XTRAN Example — Recursive vs. Iterative Factorial Computation

A recursive algorithm is one that invokes itself (recurses).  A common example is the factorial function, in which the factorial of a number n (expressed mathematically as n!) is defined as 1 if n is 1, else n times the factorial of n - 1.  (The special case for the value 1 is called the recursion's terminating condition; without such a condition, a recursive algorithm will recurse until it runs out of memory and crashes.)

A recursive algorithm in which the self-invocation is the last action in the algorithm is said to be tail-recursive.  It has been proven that any tail-recursive algorithm can be implemented using iteration instead of the recursion.  This is usually more efficient, because it eliminates the function call overhead and memory usage that are inherent in the recursion.

The following example uses an XTRAN rules file comprising 86 non-comment lines of "meta-code" (XTRAN's rules language) to compare execution times of recursive vs. iterative computation of factorials.  The rules took less than ¾ hour to write and about ¼ hour to debug.  (That's right, only 1 hour total!)

The rules repeatedly prompt for a number to do and the number of computations (to get a meaningful time result).  They then compute the factorial both recursively and iteratively the specified number of times, and show the results.

How can such powerful and generalized computation be automated in only 1 hour and only 86 code lines of XTRAN rules?  Because there is so much capability already available as part of XTRAN's rules language.  These rules take advantage of the following functionality:

• Text formatting
• Regular expression matching
• Creating new meta-functions written in meta-code, which we call user meta-functions
• Recursive user meta-functions
• Meta-variable and meta-function pointers

The input to and output from XTRAN are untouched.

---

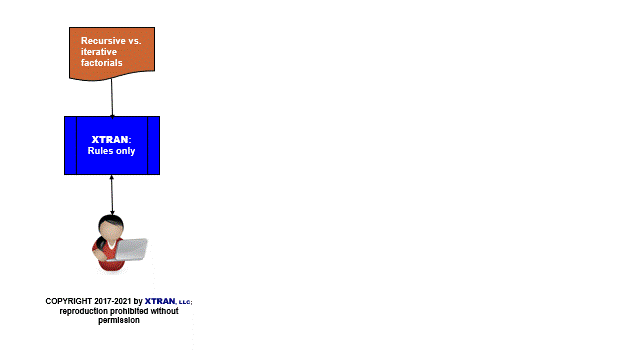
Process Flowchart

Here is a flowchart for this process, in which the elements are color coded:

• BLUE for XTRAN versions (runnable programs)
• ORANGE for XTRAN rules (text files)

---

Interactive results (this indicates user input):

Number whose n! you want, 1-10 [done]:  5<ENTER>
Number of computations:  5<ENTER>
Result:            120
Recursive:           0 seconds for 5 computations
Iterative:           0 seconds for 5 computations

Number whose n! you want, 1-10 [done]:  15<ENTER>
<BELL>?Number must be between 1 and 10!

Number whose n! you want, 1-10 [done]:  10<ENTER>
Number of computations:  1000<ENTER>
Result:        3628800
Recursive:           2 seconds for 1000 computations
Iterative:           2 seconds for 1000 computations

Number whose n! you want, 1-10 [done]:  10<ENTER>
Number of computations:  2000<ENTER>
Result:        3628800
Recursive:           4 seconds for 2000 computations
Iterative:           3 seconds for 2000 computations

Number whose n! you want, 1-10 [done]:  xyz<ENTER>
<BELL>?You must enter an integer, or just <ENTER> when done!

Number whose n! you want, 1-10 [done]:  10<ENTER>
Number of computations:  5000<ENTER>
Result:        3628800
Recursive:          12 seconds for 5000 computations
Iterative:           7 seconds for 5000 computations

Number whose n! you want, 1-10 [done]:  <ENTER>